If we were to say the word ‘interval’ to you, what would your first thought be? The theatre? Ice cream? (With you on that one.)
The basic dictionary definition of the word interval is a gap or space between two things, and in musical terms, that’s exactly what it represents: an interval is the distance in pitch between two notes.
Intervals make for a fairly broad topic, so in this guide, we’ll start with the basics and look at how to create and work out simple intervals. Essentially, there are five types of interval: major, minor, perfect, augmented and diminished. It’s the first three of these types that we’ll be examining here.
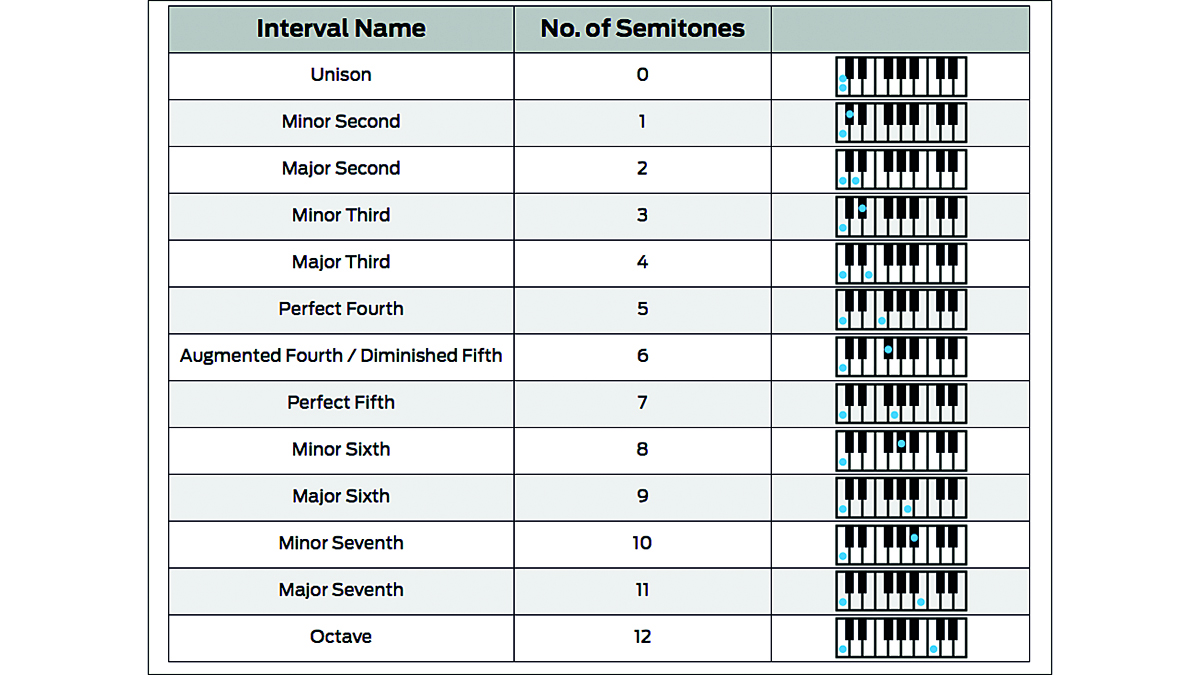
When naming musical intervals, there are two things to consider: quality and distance. Quality refers to the type of interval (major, minor, perfect, etc), while distance refers to the number of notes spanned by the interval. This can take the form of unison (both notes the same - ie, no interval), seconds, thirds, fourths, fifths, sixths, sevenths or octaves. You might have an interval of a perfect fourth or a minor third, for example.
What tends to confuse people, though, is that the number of semitones spanned by an interval doesn’t always correspond to the number in its name - for instance, a major third is actually a span of four semitones, while a perfect fifth covers seven!
To understand why this is, we need to look at the relationships between the degrees of the scale that the notes at either end of the interval are taken from - our mission is to clear up some of the confusion and get your interval identification skills polished up to a dazzling shine. Here we go…
Step 1: Let’s look again at the interval pattern for the major scale. Above is C major (C-D-E-F-G-A-B-C), and its pattern is T-T-S-T-T-T-S, so the interval between C and D is a tone, between D and E is another tone, between E and F is a semitone, and so on.
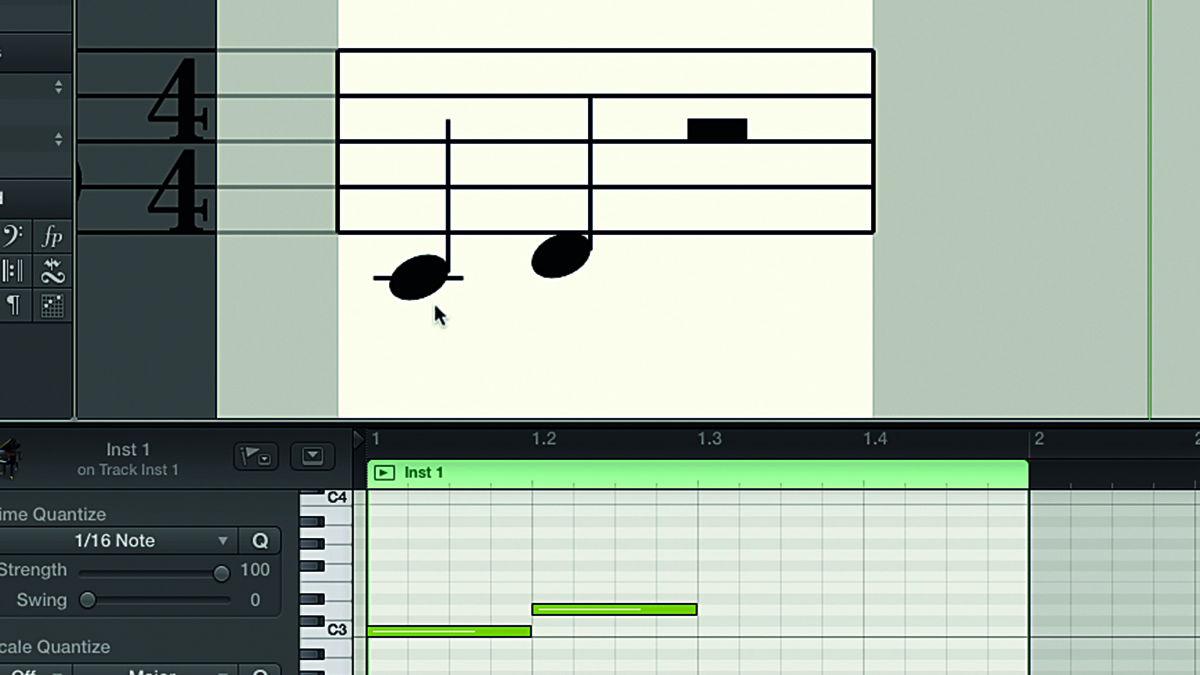
Step 2: As well as being represented by T (tone) or S (semitone), the intervals between the notes can also have other names. Let’s look at the first two notes of the scale: C and D. In order to work out what the particular interval between any two notes might be, begin by counting the letter names from the first note to the last note.
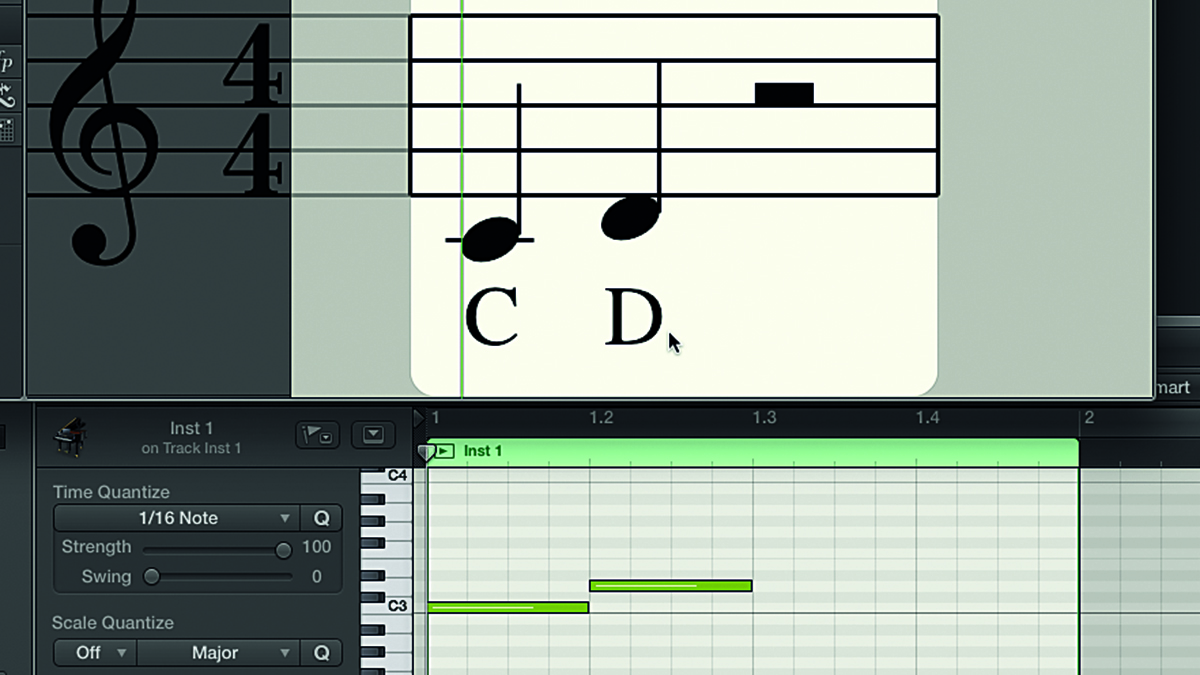
Step 3: In this case, we have C - one; and D – two. Two notes mean the interval is a second of some kind. Next, we determine the interval’s quality - whether it’s major, minor, perfect, etc. Look at the lower note and construct a major scale starting on it. The interval between the tonic (root note) of a major scale and any other note in it is always either a major or perfect interval.
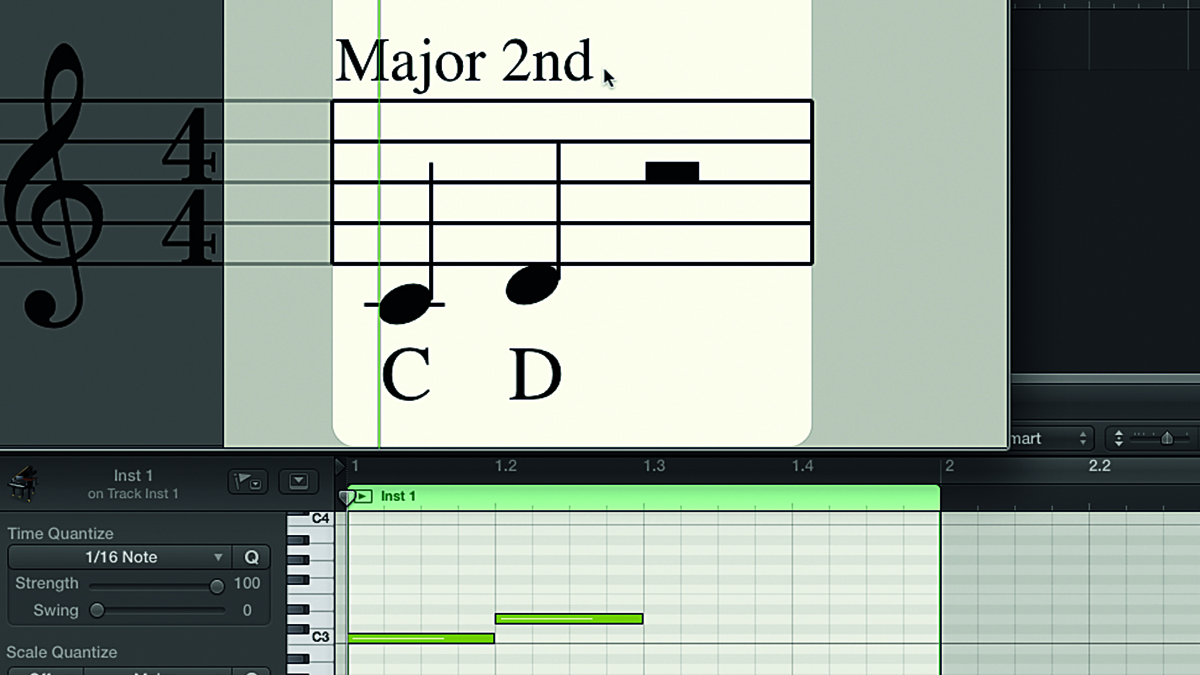
Step 4: The ‘perfect’ intervals are the unison, fourth, fifth and octave. The remaining intervals of the major scale - the second, third, sixth and seventh - are known as ‘major’ intervals. We’ve determined that this interval is a second, and we know that the upper note D is part of the C major scale, so the interval is called a major second.
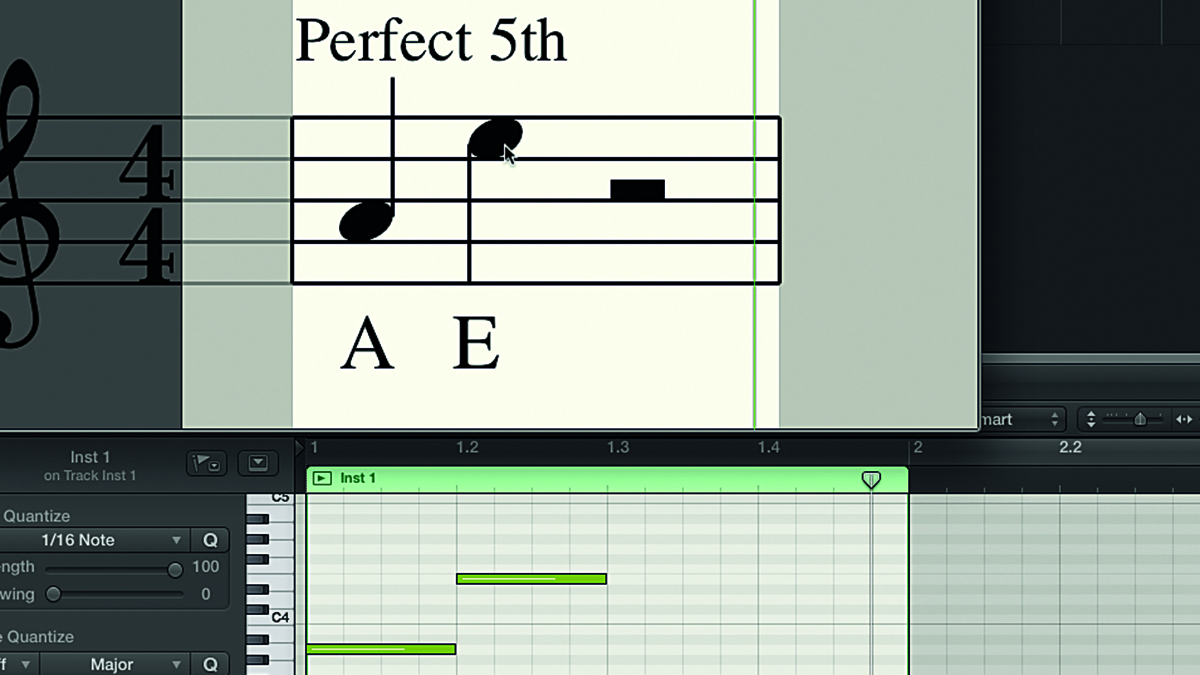
Step 5: The interval shown here is A to E. Counting the letters between the two notes gives us A, B, C, D, E, adding up to a total of five notes. This interval is therefore some kind of fifth. Since E is part of the A major scale (A, B, C#, D, E, F#, G#), we can safely say the interval is a perfect fifth. But what if the upper note is not part of the major scale built from the lower note?
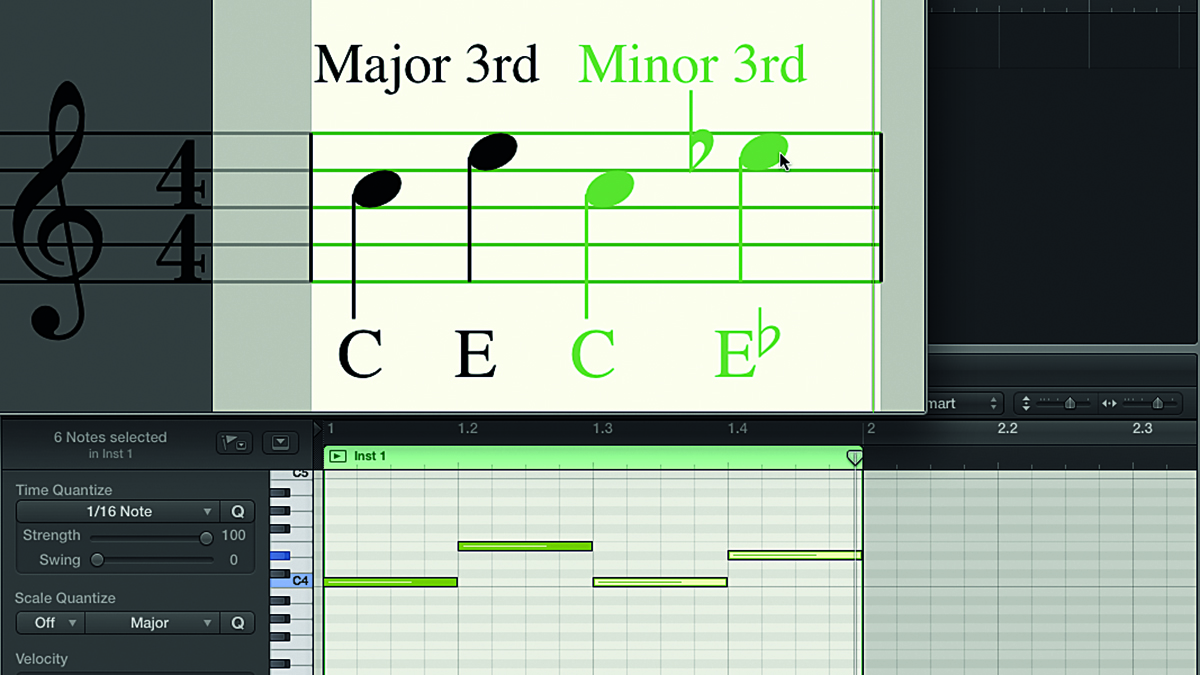
Step 6: If the interval is a semitone narrower than a major one, it’s a minor interval. C to E is a major third, as it covers three note letters (C, D, E) at the start of the C major scale. C to Eb covers the same three note letters, so it’s still a third, but because it’s a semitone narrower than a major third, it’s a minor third. Perfect intervals occur in both major and minor scales.
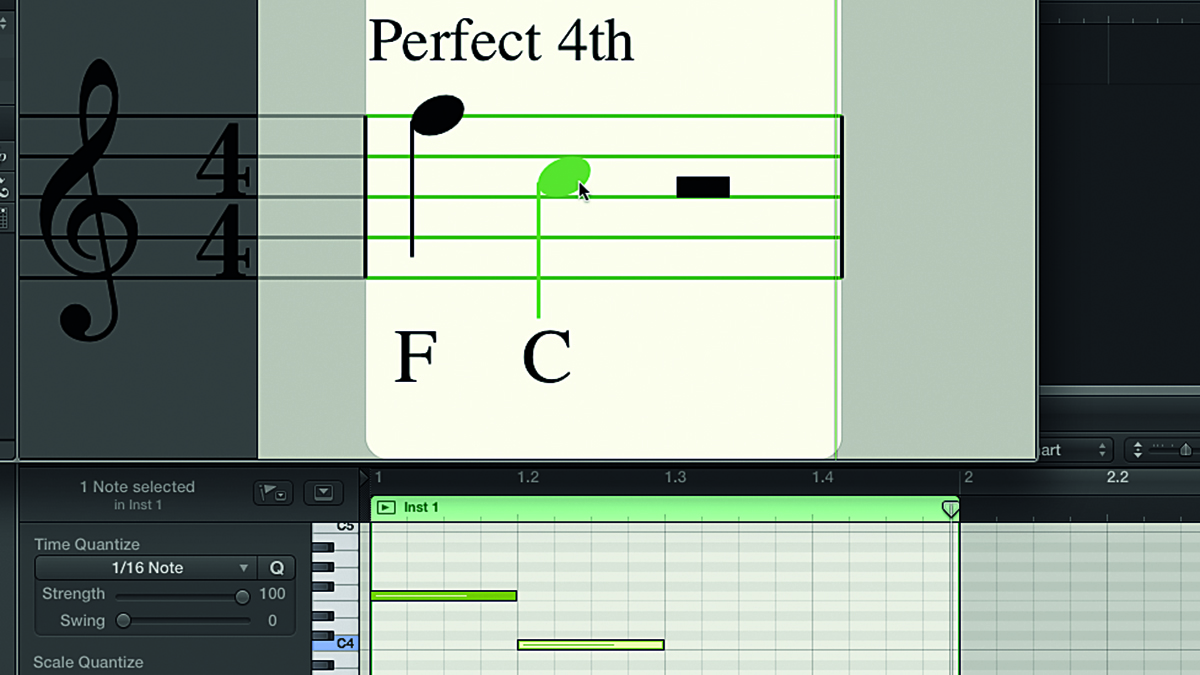
Step 7: Intervals can go down as well as up - the direction of the melody doesn’t matter, as the distance between the notes is the same. Here’s a high F followed by a low C. The interval is still a perfect fourth (F, E, D, C = four letter names). The distance between the notes is still five semitones, regardless of whether you approach from the C ascending or the F descending.
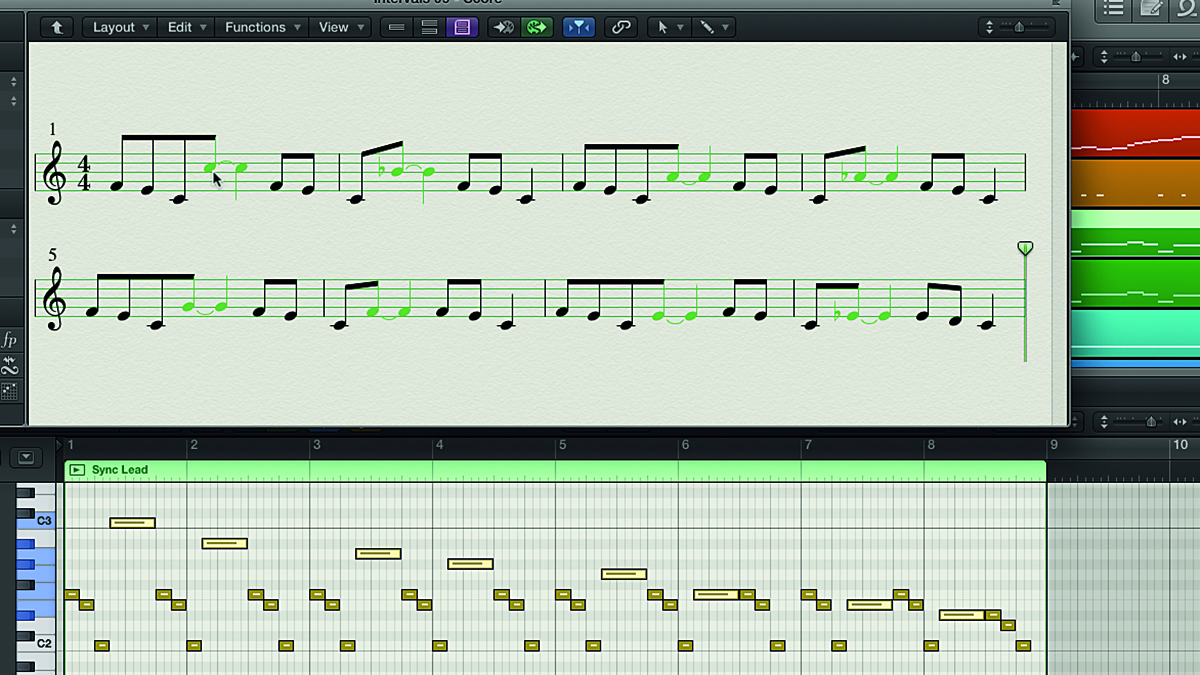
Step 8: To look at intervals in the context of a production, here’s a track made up of drums, a bass synth and a lead line. The lead synth plays a repeating motif with a different top note each time. Each time round, the top note is a semitone or two lower, creating a different interval between it and the low C note that comes before it.
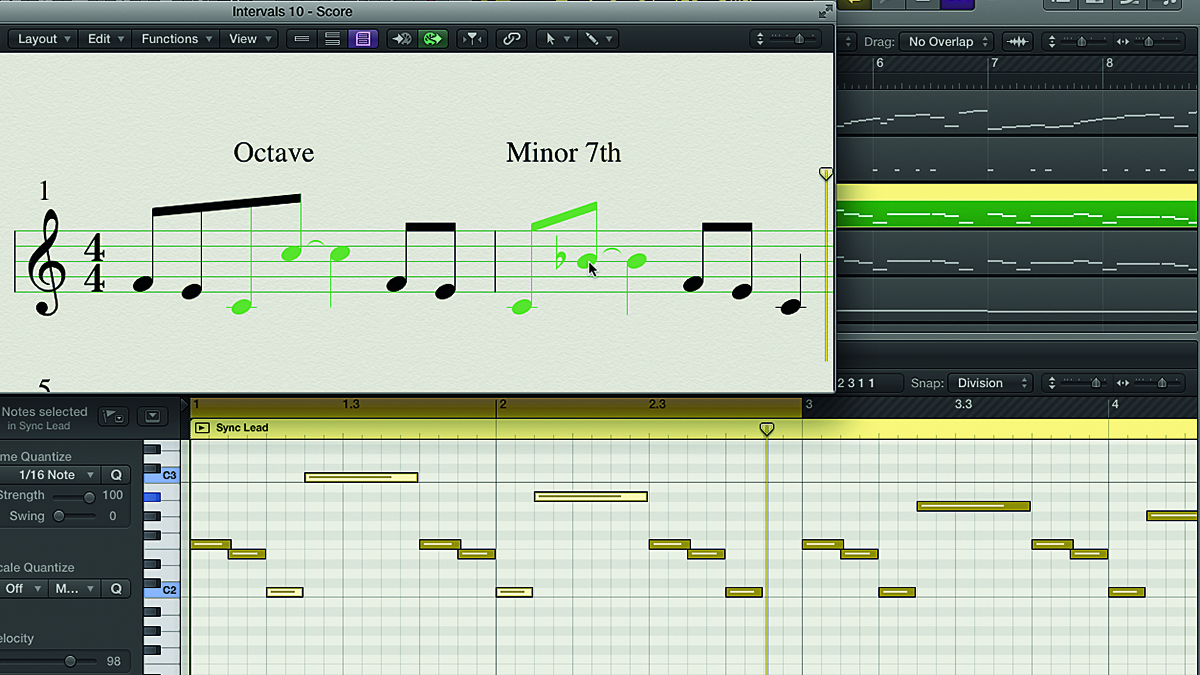
Step 9: The first interval, in bar 1, is a full octave leap from C2 to C3. In bar 2, however, the C2 is followed by a Bb2. Counting C to B, ignoring flats and sharps, gives us seven notes (C, D, E, F, G, A, B), and since the note is a Bb, that makes the interval one semitone narrower than a major seventh (11 semitones), giving us a minor seventh (10 semitones).
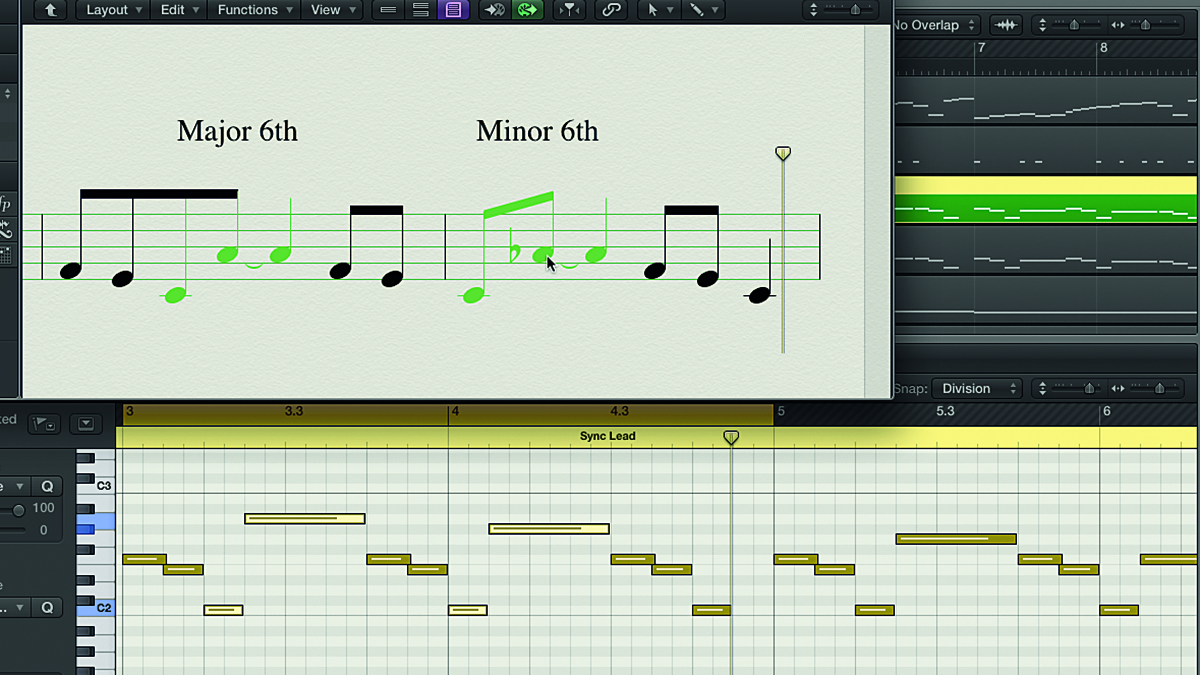
Step 10: Bar 3 has a C2 to A2 interval - a major sixth. Bar 4 drops the upper note one semitone to an Ab, narrowing the interval from a major to a minor sixth. The last four bars contain a perfect fifth (C to G) in bar 5, a perfect fourth (C to F) in bar 6, a major third (C to E) in bar 7 and a minor third (C to Eb) in Bar 8.
Interval overview
Recommended listening
There are plenty of well-known tunes whose first two notes can be used to help recognise and identify simple intervals. Most of these melodies use the named intervals at the very beginning, showing how useful intervals can be in setting the mood of a piece.
- Minor 2nd - Jaws Theme
- Major 2nd - Happy Birthday
- Minor 3rd - Greensleeves
- Major 3rd - When The Saints Go Marching In
- Perfect 4th - Here Comes The Bride
- Augmented 4th/Diminished 5th - Simpsons Theme
- Perfect 5th - Twinkle Twinkle Little Star
- Minor 6th - In My Life (The Beatles)*
- Major 6th - My Bonnie Lies Over The Ocean
- Minor 7th - Original Star Trek Theme
- Major 7th - Don’t Know Why (Norah Jones)
- Octave - Somewhere Over The Rainbow
Pro tips
Inverted intervals
Not to be confused with descending intervals, inverted intervals are what you get if you shift either the lower note up one octave or the upper note down one octave, swapping their relative positions. When you do this, major intervals become minor, minor intervals become major and perfect intervals remain perfect. The interval number and the number of its inversion always add up to nine - if low C to high E is a major third, low E to high C must be a minor sixth (3+6=9).
Melodic, harmonic and compound intervals
Melodic intervals are made up of two notes played one after the other, whereas harmonic intervals are made up of notes played simultaneously. Compound intervals are intervals wider than an octave. A major tenth (or a ‘compound major third’) spans 16 semitones (eg, C2-E3), equal to one octave plus one major third.
